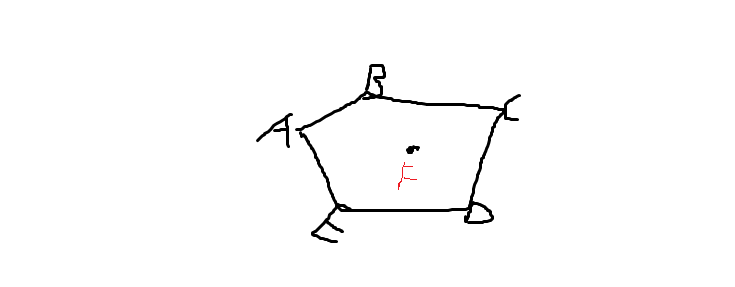
中心点: F
  多变形顶点: A、B、C、 D  、E
  离中心点最近半径长度为：t
  离中心点最远半径长度为：y
  当前所处于的点: K

1.判断当前K点到中心点F的距离 >=  y，则不在多边形内。
2.判断当前K点到中心点F的距离 <= t, 则说明在多边形内
3.迭代所有边，依次和当前点比较，判断是否都在同一侧，如果是则在多边形内，否则不在多变形内。

/**
 * 检测点是否在多边形内
 * @param point 需要检测的点
 * @return 点是否在多边形内
 */
public boolean checkIsInside(Vector3D point) {
    if (!isEnable) {
        return false;
    }

    if (vertices.size() <= 2) {
        return false;
    }

    //判断距离
    double disToCenter = point.distance2D(center);
    if (disToCenter >= outerRadius) {
        return false;
    } else if (disToCenter <= innerRadius) {
        return true;
    }

    boolean preSide = false;

    //.迭代所有边，依次和当前点比较，判断是否都在同一侧，如果是则在多边形内，否则不在多变形内。
    for (int i = 0; i < vertices.size(); ++i) {
        Vector2D lineStart = vertices.get(i);
        //i 是当前循环迭代中的索引，表示当前处理的多边形的顶点。
        //(i + 1) % vertices.size() 计算的是下一个顶点的索引。这里使用了模运算 % vertices.size() 来确保索引不会超出顶点列表的范围，因为多边形是一个封闭的图形，最后一个顶点的下一个顶点应该是第一个顶点。
        //vertices.get((i + 1) % vertices.size()) 表示从顶点列表中获取下一个顶点的坐标，即多边形的当前边的结束点。
        Vector2D lineEnd = vertices.get((i + 1) % vertices.size());

        boolean curSide = checkIsAtLeftSide(point, lineStart, lineEnd);
        if (0 == i) {
            preSide = curSide;
        } else {
            if (preSide != curSide) {
                return false;
            }
        }
    }

    return true;
}

/**
 * 检测点是否在线段的左侧
 * @param point     需要检测的点
 * @param lineStart 线段的起点
 * @param lineEnd   线段的终点
 * @return 是否在线段的左侧
 */
private boolean checkIsAtLeftSide(Vector3D point, Vector2D lineStart, Vector2D lineEnd) {
    Vector2D vec1 = new Vector2D(point.x - lineStart.x, point.y - lineStart.y);
    Vector2D vec2 = lineEnd.sub(lineStart);

    double crossProduct = vec1.x * vec2.y - vec1.y * vec2.x;

    return crossProduct < 0;
}