服务器寻路03-a*代码实现
目录
A*代码实现
1.网上有很多A*代码实现
网上有很多A*代码实现,但是java版本的比较少,并且代码质量参差不齐,我这里找了个github上的还可以:
https://github.com/marcelo-s/A-Star-Java-Implementation
代码不错,并且逻辑正确,思路清晰。
2.加了中文注释后的代码
1.1.AStar类
package org.example;
import java.util.*;
/**
* A Star Algorithm
*
* 1. 把起点加入 open list 。
* 2. 重复如下过程:
* a. 遍历 open list ,查找 F 值最小的节点,把它作为当前要处理的节点。
* b. 把这个节点移到 close list 。
* c. 对当前方格的 8 个相邻方格的每一个方格?
* ◆ 如果它是不可抵达的或者它在 close list 中,忽略它。否则,做如下操作。
* ◆ 如果它不在 open list 中,把它加入 open list ,并且把当前方格设置为它的父亲,记录该方格的 F , G 和 H 值。
* ◆ 如果它已经在 open list 中,检查这条路径 ( 即经由当前方格到达它那里 ) 是否更好,用 G 值作参考。更小的 G 值表示这是更好的路径。
* 如果是这样,把它的父亲设置为当前方格,并重新计算它的 G 和 F 值。如果你的 open list 是按 F 值排序的话,改变后你可能需要重新排序。
* d. 停止,当你:
* ◆ 把终点加入到了 open list 中,此时路径已经找到了,或者
* ◆ 查找终点失败,并且 open list 是空的,此时没有路径。
* 3. 保存路径。从终点开始,每个方格沿着父节点移动直至起点,这就是你的路径。
*
* @author Marcelo Surriabre
* @version 2.1, 2017-02-23
*/
public class AStar {
/**
* 水平和垂直移动代价常量
*/
private static int DEFAULT_HV_COST = 10; // Horizontal - Vertical Cost
/**
* 对角移动代价常量
*/
private static int DEFAULT_DIAGONAL_COST = 14;
/**
* 移动代价
*/
private int hvCost;
private int diagonalCost;
/**
* 搜索区域节点
*/
private Node[][] searchArea;
/**
* 开放列表。PriorityQueue优先队列,底层其实就是小根堆
*/
private PriorityQueue<Node> openList;
/**
* 关闭列表
*/
private Set<Node> closedSet;
/**
* 初始节点
*/
private Node initialNode;
/**
* 最终节点
*/
private Node finalNode;
public AStar(int rows, int cols, Node initialNode, Node finalNode, int hvCost, int diagonalCost) {
this.hvCost = hvCost;
this.diagonalCost = diagonalCost;
//设置初始和最终节点,因为是起点和终点所以不需要计算当前节点的H值
setInitialNode(initialNode);
setFinalNode(finalNode);
this.searchArea = new Node[rows][cols];
//开放列表,优先队列,F值最小的优先弹出
this.openList = new PriorityQueue<Node>(new Comparator<Node>() {
@Override
public int compare(Node node0, Node node1) {
return Integer.compare(node0.getF(), node1.getF());
}
});
setNodes();
this.closedSet = new HashSet<>();
}
public AStar(int rows, int cols, Node initialNode, Node finalNode) {
this(rows, cols, initialNode, finalNode, DEFAULT_HV_COST, DEFAULT_DIAGONAL_COST);
}
/**
* 迭代搜索区域二维数组,并计算每个Node的H值
*/
private void setNodes() {
for (int i = 0; i < searchArea.length; i++) {
for (int j = 0; j < searchArea[0].length; j++) {
Node node = new Node(i, j);
//计算h值大小
node.calculateHeuristic(getFinalNode());
this.searchArea[i][j] = node;
}
}
}
/**
* 设置阻挡
* @param blocksArray
*/
public void setBlocks(int[][] blocksArray) {
for (int i = 0; i < blocksArray.length; i++) {
int row = blocksArray[i][0];
int col = blocksArray[i][1];
setBlock(row, col);
}
}
/**
* 寻路方法
* @return
*/
public List<Node> findPath() {
//先将起点加入到开放列表里
openList.add(initialNode);
while (!isEmpty(openList)) {
//弹出F值最小的节点
Node currentNode = openList.poll();
if (null == currentNode) {
continue;
}
//加到关闭列表
closedSet.add(currentNode);
if (isFinalNode(currentNode)) {
//如果当前点是终点,回溯获取移动路径
return getPath(currentNode);
} else {
//当前点不是终点,添加相邻节点信息
addAdjacentNodes(currentNode);
}
}
return new ArrayList<Node>();
}
/**
* 回溯获取路径
* @param currentNode
* @return
*/
private List<Node> getPath(Node currentNode) {
List<Node> path = new ArrayList<Node>();
path.add(currentNode);
Node parent;
//寻找父节点
while ((parent = currentNode.getParent()) != null) {
path.add(0, parent);
currentNode = parent;
}
return path;
}
/**
* 添加相邻节点信息
*
* <>
* 以当前点为中心:
* 上方:2个格子
* 中间(同一行): 2个格子
* 下方:3个格子
* </>
* @param currentNode
*/
private void addAdjacentNodes(Node currentNode) {
addAdjacentUpperRow(currentNode);
addAdjacentMiddleRow(currentNode);
addAdjacentLowerRow(currentNode);
}
private void addAdjacentLowerRow(Node currentNode) {
int row = currentNode.getRow();
int col = currentNode.getCol();
int lowerRow = row + 1;
if (lowerRow < getSearchArea().length) {
if (col - 1 >= 0) {
checkNode(currentNode, col - 1, lowerRow, getDiagonalCost()); // Comment this line if diagonal movements are not allowed
}
if (col + 1 < getSearchArea()[0].length) {
checkNode(currentNode, col + 1, lowerRow, getDiagonalCost()); // Comment this line if diagonal movements are not allowed
}
checkNode(currentNode, col, lowerRow, getHvCost());
}
}
private void addAdjacentMiddleRow(Node currentNode) {
int row = currentNode.getRow();
int col = currentNode.getCol();
int middleRow = row;
if (col - 1 >= 0) {
checkNode(currentNode, col - 1, middleRow, getHvCost());
}
if (col + 1 < getSearchArea()[0].length) {
checkNode(currentNode, col + 1, middleRow, getHvCost());
}
}
/**
* 添加相邻的上方节点信息
* @param currentNode 当前节点
*/
private void addAdjacentUpperRow(Node currentNode) {
int row = currentNode.getRow();
int col = currentNode.getCol();
//上方节点行索引
int upperRow = row - 1;
if (upperRow >= 0) {
if (col - 1 >= 0) {
//左上方节点, 传入的移动代价为对角移动代价也就是14
checkNode(currentNode, col - 1, upperRow, getDiagonalCost()); // Comment this if diagonal movements are not allowed
}
if (col + 1 < getSearchArea()[0].length) {
//右上方节点,传入的移动代价为对角移动代价也就是14
checkNode(currentNode, col + 1, upperRow, getDiagonalCost()); // Comment this if diagonal movements are not allowed
}
//正上方节点,传入的移动代价为垂直移动代价也就是10
checkNode(currentNode, col, upperRow, getHvCost());
}
}
/**
* c. 对当前方格的 8 个相邻方格的每一个方格?
* ◆ 如果它是不可抵达的或者它在 close list 中,忽略它。否则,做如下操作。
* ◆ 如果它不在 open list 中,把它加入 open list ,并且把当前方格设置为它的父亲,记录该方格的 F , G 和 H 值。
* ◆ 如果它已经在 open list 中,检查这条路径 ( 即经由当前方格到达它那里 ) 是否更好,用 G 值作参考。更小的 G 值表示这是更好的路径。
* 如果是这样,把它的父亲设置为当前方格,并重新计算它的 G 和 F 值。如果你的 open list 是按 F 值排序的话,改变后你可能需要重新排序。
* @param currentNode
* @param col
* @param row
* @param cost
*/
private void checkNode(Node currentNode, int col, int row, int cost) {
//获取相邻节点信息
Node adjacentNode = getSearchArea()[row][col];
//节点不是阻挡并且不在关闭列表
if (!adjacentNode.isBlock() && !getClosedSet().contains(adjacentNode)) {
//如果开放列表里不包含当前相邻节点
if (!getOpenList().contains(adjacentNode)) {
adjacentNode.setNodeData(currentNode, cost);
getOpenList().add(adjacentNode);
} else {
//开放列表里已经包含了当前相邻节点
boolean changed = adjacentNode.checkBetterPath(currentNode, cost);
if (changed) {
// Remove and Add the changed node, so that the PriorityQueue can sort again its
// contents with the modified "finalCost" value of the modified node
//先删除然后再添加。可以保证队列重新排序一次
getOpenList().remove(adjacentNode);
getOpenList().add(adjacentNode);
}
}
}
}
private boolean isFinalNode(Node currentNode) {
return currentNode.equals(finalNode);
}
private boolean isEmpty(PriorityQueue<Node> openList) {
return openList.size() == 0;
}
private void setBlock(int row, int col) {
this.searchArea[row][col].setBlock(true);
}
public Node getInitialNode() {
return initialNode;
}
public void setInitialNode(Node initialNode) {
this.initialNode = initialNode;
}
public Node getFinalNode() {
return finalNode;
}
public void setFinalNode(Node finalNode) {
this.finalNode = finalNode;
}
public Node[][] getSearchArea() {
return searchArea;
}
public void setSearchArea(Node[][] searchArea) {
this.searchArea = searchArea;
}
public PriorityQueue<Node> getOpenList() {
return openList;
}
public void setOpenList(PriorityQueue<Node> openList) {
this.openList = openList;
}
public Set<Node> getClosedSet() {
return closedSet;
}
public void setClosedSet(Set<Node> closedSet) {
this.closedSet = closedSet;
}
public int getHvCost() {
return hvCost;
}
public void setHvCost(int hvCost) {
this.hvCost = hvCost;
}
private int getDiagonalCost() {
return diagonalCost;
}
private void setDiagonalCost(int diagonalCost) {
this.diagonalCost = diagonalCost;
}
}
2.Node类
package org.example;
/**
* Node Class
*
* @author Marcelo Surriabre
* @version 2.0, 2018-02-23
*/
public class Node {
/**
* 估值 f = g + h
*/
private int g;
private int f;
private int h;
/**
* 行坐标索引
*/
private int row;
/**
* 列坐标索引
*/
private int col;
/**
* 是否阻挡
*/
private boolean isBlock;
/**
* 父节点(回溯用,终点往起点找)
*/
private Node parent;
public Node(int row, int col) {
super();
this.row = row;
this.col = col;
}
/**
* 计算h值大小(曼哈顿算法)
*
* <>
* 直接用终点和当前点坐计算
* </>
* @param finalNode 终点Node
*/
public void calculateHeuristic(Node finalNode) {
//这里其实不用太纠结实际走多少个格子,因为所有的h值用一个计算公式,多走一个或少一个意义最终没区别。
this.h = Math.abs(finalNode.getRow() - getRow()) + Math.abs(finalNode.getCol() - getCol());
}
public void setNodeData(Node currentNode, int cost) {
int gCost = currentNode.getG() + cost;
setParent(currentNode);
setG(gCost);
calculateFinalCost();
}
/**
* 检测是否有更好的g值
* @param currentNode
* @param cost
* @return
*/
public boolean checkBetterPath(Node currentNode, int cost) {
int gCost = currentNode.getG() + cost;
//当前节点走到相邻节点(假设:B),消耗的g值小于B本来的g值,说明路径更好。
// 需要重新设置B节点父节点和重新计算B节点的g值、h值
if (gCost < getG()) {
setNodeData(currentNode, cost);
return true;
}
return false;
}
private void calculateFinalCost() {
int finalCost = getG() + getH();
setF(finalCost);
}
@Override
public boolean equals(Object arg0) {
Node other = (Node) arg0;
return this.getRow() == other.getRow() && this.getCol() == other.getCol();
}
@Override
public String toString() {
return "Node [row=" + row + ", col=" + col + "]";
}
public int getH() {
return h;
}
public void setH(int h) {
this.h = h;
}
public int getG() {
return g;
}
public void setG(int g) {
this.g = g;
}
public int getF() {
return f;
}
public void setF(int f) {
this.f = f;
}
public Node getParent() {
return parent;
}
public void setParent(Node parent) {
this.parent = parent;
}
public boolean isBlock() {
return isBlock;
}
public void setBlock(boolean isBlock) {
this.isBlock = isBlock;
}
public int getRow() {
return row;
}
public void setRow(int row) {
this.row = row;
}
public int getCol() {
return col;
}
public void setCol(int col) {
this.col = col;
}
}
3.测试方法
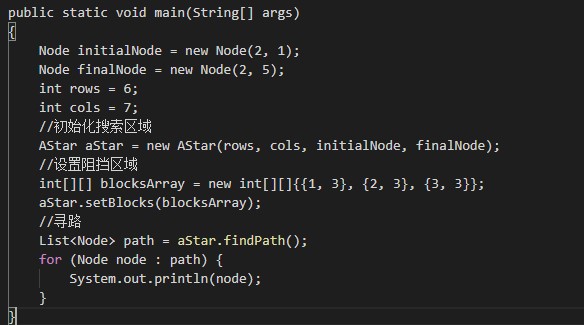
用图片展示吧,上面有特殊符号会引起博客报错。
4.结果
//Search Area
// 0 1 2 3 4 5 6
// 0 - - - - - - -
// 1 - - - B - - -
// 2 - I - B - F -
// 3 - - - B - - -
// 4 - - - - - - -
// 5 - - - - - - -
//Expected output with diagonals
//Node [row=2, col=1]
//Node [row=1, col=2]
//Node [row=0, col=3]
//Node [row=1, col=4]
//Node [row=2, col=5]
//Search Path with diagonals
// 0 1 2 3 4 5 6
// 0 - - - * - - -
// 1 - - * B * - -
// 2 - I* - B - *F -
// 3 - - - B - - -
// 4 - - - - - - -
// 5 - - - - - - -
//Expected output without diagonals
//Node [row=2, col=1]
//Node [row=2, col=2]
//Node [row=1, col=2]
//Node [row=0, col=2]
//Node [row=0, col=3]
//Node [row=0, col=4]
//Node [row=1, col=4]
//Node [row=2, col=4]
//Node [row=2, col=5]
//Search Path without diagonals
// 0 1 2 3 4 5 6
// 0 - - * * * - -
// 1 - - * B * - -
// 2 - I* * B * *F -
// 3 - - - B - - -
// 4 - - - - - - -
// 5 - - - - - - -
3.总结
代码只是最基础的实现,可以帮助我们理解A星算法,但离真正的游戏线上寻路还有很大距离。
比如:
1.代码上直接用了优先队列PriorityQueue,而实际上我们会自己实现一个类似四叉树的小根堆,以提高效率。
2.真实的线上还会利用漏斗算法。
。。。
后面我们继续探索。